These shape functions are either a direct 4-node tetrahedral such as SOLID285 or a condensation of an 8-node brick element such as SOLID5, FLUID30, or SOLID98.

Figure 11.10:  3-D Solid Elements

The resulting effective shape functions are:

(11–172)

(11–173)

(11–174)

(11–175)

(11–176)

(11–177)

(11–178)

(11–179)

(11–180)

(11–181)

(11–182)

(11–183)

These shape functions are for 10-node tetrahedron elements such as SOLID98 and SOLID227, or by condensation for SOLID90.

Figure 11.11:  10-Node Tetrahedra Element

(11–184)

(11–185)

(11–186)

(11–187)

(11–188)

(11–189)

(11–190)

This element is a condensation of an 8-node brick element.

Figure 11.12:  8-Node Brick Element

The resulting effective shape functions are:

(11–191)

These shape functions are for 13-node pyramid elements which are based on a condensation of a 20-node brick element:

Figure 11.13:  13-Node Pyramid Element

(11–192)

(11–193)

(11–194)

(11–195)

(11–196)

(11–197)

Figure 11.14:  6-Node Wedge Element

The 6-node wedge elements are a condensation of an 8-node brick such as SOLID5 or FLUID30. These shape functions are for 6-node wedge elements without extra shape functions:

(11–198)

(11–199)

(11–200)

(11–201)

(11–202)

(11–203)

(11–204)

The 6-node wedge elements are a condensation of an 8-node brick such as SOLID5. (See Figure 11.14: 6-Node Wedge Element.) These shape functions are for 6-node wedge elements with extra shape functions:

(11–205)

(11–206)

(11–207)

These shape functions are for 15-node wedge elements such as SOLID90 that are based on a condensation of a 20-node brick element Equation 11–232. or are computed directly.

Figure 11.15:  15-Node Wedge Element

Elements in a wedge configuration use shape functions based on triangular coordinates and the r coordinate going from -1.0 to +1.0.

(11–208)

(11–209)

(11–210)

(11–211)

(11–212)

(11–213)

Figure 11.16:  8-Node Brick Element

These shape functions are for 8-node brick elements without extra shape functions such as SOLID5 with KEYOPT(3) = 1 or FLUID30:

(11–214)

(11–215)

(11–216)

(11–217)

(11–218)

(11–219)

(11–220)

(11–221)

(11–222)

(11–223)

(11–224)

(11–225)

(11–226)

(11–227)

(11–228)

(Please see Figure 11.16: 8-Node Brick Element) These shape functions are for 8-node brick elements with extra shape functions such as SOLID5 with KEYOPT(3) = 0:

(11–229)

(11–230)

(11–231)

Figure 11.17:  20-Node Brick Element

These shape functions are used for 20-node solid elements such as SOLID90:

(11–232)

(11–233)

(11–234)

(11–235)

(11–236)

(11–237)

(11–238)

Figure 11.18:  3-D 8-Node Brick Element

These shape functions and mapping functions are for the 3-D 8-node solid brick infinite elements such as INFIN111:

11.9.11.1. Shape Functions

(11–239)

(11–240)

(11–241)

(11–242)

(11–243)

(11–244)

(11–245)

(11–246)

11.9.11.2. Mapping Functions

(11–247)

(11–248)

(11–249)

(11–250)

Figure 11.19:  20-Node Solid Brick Infinite Element

These shape functions and mapping functions are for the 3-D 20-node solid brick infinite elements such as INFIN111:

11.9.12.1. Shape Functions

(11–251)

(11–252)

(11–253)

(11–254)

(11–255)

(11–256)

(11–257)

(11–258)

(11–259)

11.9.12.2. Mapping Functions

(11–260)

(11–261)

(11–262)

The shape and mapping functions for the nodes U, V, W, X, Y, Z, A, and B are deliberately set to zero.

This section contains shape functions for general axisymmetric solid elements. These elements are available in a number of configurations, including certain combinations of the following features:

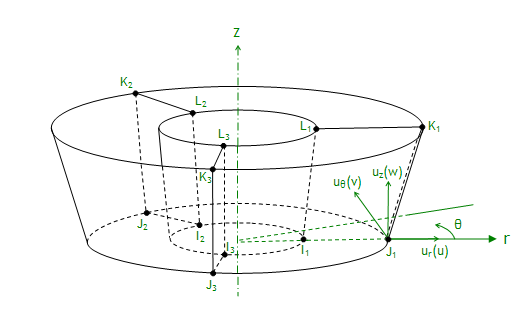
The elemental coordinates are cylindrical coordinates and displacements are defined and interpolated in that coordinate system, as shown in Figure 11.20: General Axisymmetric Solid Elements (when N_np = 3).

Figure 11.20:  General Axisymmetric Solid Elements (when N_np = 3)

When N_np is an odd number, the interpolation function used for displacement is:

(11–263)

where:

i = r, θ, z

hi (s, t) = regular Lagrangian polynominal interpolation functions like Equation 11–120 or Equation 11–134.

= coefficients for the Fourier terms.

When N_np is an even number, the interpolation function is:

(11–264)

The temperatures are interpolated by Lagrangian polynominal interpolations in s, t plane, and linearly interpolated with θ in circumferential (θ) direction as:

(11–265)

where:

= node plane number in circumferential direction

Tn = same as Equation 11–128 and Equation 11–138.

11.9.13.1. General Axisymmetric Solid with 4 Base Nodes

All of the coefficients in Equation 11–263 and Equation 11–264 can be expressed by node displacements. Using u_r = u, u_j = v, u_z = w, and take N_np = 3 as an example.

(11–266)

(11–267)

(11–268)

11.9.13.2. General Axisymmetric Solid with 3 Base Nodes

(11–269)

(11–270)

(11–271)

11.9.13.3. General Axisymmetric Solid with 8 Base Nodes

Similar to the element with 4 base nodes, the u, v, and w are expressed as:

(11–272)

(11–273)

(11–274)

11.9.13.4. General Axisymmetric Solid with 6 Base Nodes

(11–275)

(11–276)

(11–277)