Rate-independent plasticity is characterized by the irreversible straining that occurs in a material once a certain level of stress is reached. The plastic strains are assumed to develop instantaneously, that is, independent of time. Several options are available to characterize different types of material behaviors:
Material Behavior Option
Bilinear Isotropic Hardening
Multilinear Isotropic Hardening
Nonlinear Isotropic Hardening
Classical Bilinear Kinematic Hardening
Multilinear Kinematic Hardening
Nonlinear Kinematic Hardening
Anisotropic
Drucker-Prager
Cast Iron
User-specified behavior (as described in User Routines and Non-Standard Uses in the Advanced Analysis Guide and in the Guide to ANSYS User Programmable Features)
Except for user-specified behavior (TB,USER), each material-behavior option is explained in greater detail later in this chapter. Figure 4.1: Stress-Strain Behavior of Each of the Plasticity Options represents the stress-strain behavior of each of the options.
Plasticity theory provides a mathematical relationship that characterizes the elastoplastic response of materials. There are three ingredients in the rate-independent plasticity theory: the yield criterion, flow rule and the hardening rule. These will be discussed in detail subsequently. Table 4.1: Notation summarizes the notation used in the remainder of this chapter.
The yield criterion determines the stress level at which yielding is initiated. For multi-component stresses, this is represented as a function of the individual components, f({σ}), which can be interpreted as an equivalent stress σe:
(4–4) |
where:
| {σ} = stress vector |
Table 4.1: Notation
| Variable | Definition | ANSYS Output Label |
|---|---|---|
| {εel} | elastic strains | EPEL |
| {εpl} | plastic strains | EPPL |
| {εtr} | trial strain | |
|
| equivalent plastic strain | EPEQ |
| {σ} | stresses | S |
| σe | equivalent stress | |
| σy | material yield parameter | |
| σm | mean or hydrostatic stress | HPRES |
|
| equivalent stress parameter | SEPL |
| λ | plastic multiplier | |
| {α} | yield surface translation | |
| κ | plastic work | |
| C | translation multiplier | |
| [D] | stress-strain matrix | |
| ET | tangent modulus | |
| F | yield criterion | |
| N | stress ratio | SRAT |
| Q | plastic potential | |
| {S} | deviatoric stress |
When the equivalent stress is equal to a material yield parameter σy,
(4–5) |
the material will develop plastic strains. If σe is less than σy, the material is elastic and the stresses will develop according to the elastic stress-strain relations. Note that the equivalent stress can never exceed the material yield since in this case plastic strains would develop instantaneously, thereby reducing the stress to the material yield. Equation 4–5 can be plotted in stress space as shown in Figure 4.2: Various Yield Surfaces for some of the plasticity options. The surfaces in Figure 4.2: Various Yield Surfaces are known as the yield surfaces and any stress state inside the surface is elastic, that is, they do not cause plastic strains.
The flow rule determines the direction of plastic straining and is given as:
(4–6) |
where:
| λ = plastic multiplier (which determines the amount of plastic straining) |
| Q = function of stress termed the plastic potential (which determines the direction of plastic straining) |
If Q is the yield function (as is normally assumed), the flow rule is termed associative and the plastic strains occur in a direction normal to the yield surface.
The hardening rule describes the changing of the yield surface with progressive yielding, so that the conditions (i.e. stress states) for subsequent yielding can be established. Two hardening rules are available: work (or isotropic) hardening and kinematic hardening. In work hardening, the yield surface remains centered about its initial centerline and expands in size as the plastic strains develop. For materials with isotropic plastic behavior this is termed isotropic hardening and is shown in Figure 4.3: Types of Hardening Rules (a). Kinematic hardening assumes that the yield surface remains constant in size and the surface translates in stress space with progressive yielding, as shown in Figure 4.3: Types of Hardening Rules (b).
The yield criterion, flow rule and hardening rule for each option are summarized in Table 4.2: Summary of Plasticity Options and are discussed in detail later in this chapter.
Table 4.2: Summary of Plasticity Options
| Name | TB Lab | Yield Criterion | Flow Rule | Hardening Rule | Material Response |
|---|---|---|---|---|---|
| Bilinear Isotropic Hardening | BISO | von Mises/Hill | associative | work hardening | bilinear |
| Nonlinear Isotropic Hardening | NLISO | von Mises/Hill | associative | work hardening | nonlinear |
| Classical Bilinear Kinematic Hardening | BKIN | von Mises/Hill | associative (Prandtl- Reuss equations) | kinematic hardening | bilinear |
| Nonlinear Kinematic Hardening | CHAB | von Mises/Hill | associative | kinematic hardening | nonlinear |
| Drucker- Prager | DP | von Mises with dependence on hydrostatic stress | associative or non- associative | none | elastic- perfectly plastic |
| Extended Drucker-Prager | EDP | von MIses with dependence on hydrostatic stress | associative or non- associative | work hardening | multilinear |
| Cast Iron | CAST | von Mises with dependence on hydrostatic stress | non- associative | work hardening | multilinear |
| Gurson | GURS | von Mises with dependence pressure and porosity | associative | work hardening | multilinear |
If the equivalent stress computed using elastic properties exceeds the material yield, then plastic straining must occur. Plastic strains reduce the stress state so that it satisfies the yield criterion, Equation 4–5. Based on the theory presented in the previous section, the plastic strain increment is readily calculated.
The hardening rule states that the yield criterion changes with work hardening and/or with kinematic hardening. Incorporating these dependencies into Equation 4–5, and recasting it into the following form:
(4–7) |
where:
| κ = plastic work |
| {α} = translation of yield surface |
κ and {α} are termed internal or state variables. Specifically, the plastic work is the sum of the plastic work done over the history of loading:
(4–8) |
where:
and translation (or shift) of the yield surface is also history dependent and is given as:
(4–9) |
where:
| C = material parameter |
| {α} = back stress (location of the center of the yield surface) |
Equation 4–7 can be differentiated so that the consistency condition is:
(4–10) |
Noting from Equation 4–8 that
(4–11) |
and from Equation 4–9 that
(4–12) |
Equation 4–10 becomes
(4–13) |
The stress increment can be computed via the elastic stress-strain relations
(4–14) |
where:
| [D] = stress-strain matrix |
with
(4–15) |
since the total strain increment can be divided into an elastic and plastic part. Substituting Equation 4–6 into Equation 4–13 and Equation 4–15 and combining Equation 4–13, Equation 4–14, and Equation 4–15 yields
(4–16) |
The size of the plastic strain increment is therefore related to the total increment in strain, the current stress state, and the specific forms of the yield and potential surfaces. The plastic strain increment is then computed using Equation 4–6:
(4–17) |
An Euler backward scheme is used to enforce the consistency condition Equation 4–10. This ensures that the updated stress, strains and internal variables are on the yield surface. The algorithm proceeds as follows:
The material parameter σy Equation 4–5 is determined for this time step (e.g., the yield stress at the current temperature).
The stresses are computed based on the trial strain {εtr}, which is the total strain minus the plastic strain from the previous time point (thermal and other effects are ignored):
(4–18)
where the superscripts are described with Understanding Theory Reference Notation and subscripts refer to the time point. Where all terms refer to the current time point, the subscript is dropped. The trial stress is then
(4–19)
The equivalent stress σe is evaluated at this stress level by Equation 4–4. If σe is less than σy the material is elastic and no plastic strain increment is computed.
If the stress exceeds the material yield, the plastic multiplier λ is determined by a local Newton-Raphson iteration procedure (Simo and Taylor([155])).
{Δεpl} is computed via Equation 4–17.
The current plastic strain is updated
(4–20)
where:
= current plastic strains (output as EPPL)
and the elastic strain computed
(4–21)
where:
εel = elastic strains (output as EPEL) The stress vector is:
(4–22)
where:
{σ} = stresses (output as S) The increments in the plastic work Δκ and the center of the yield surface {Δα} are computed via Equation 4–11 and Equation 4–12 and the current values updated
(4–23)
and
(4–24)
where the subscript n-1 refers to the values at the previous time point.
For output purposes, an equivalent plastic strain
(output as EPEQ), equivalent plastic strain increment Δ
(output with the label “MAX PLASTIC STRAIN STEP”), equivalent stress parameter
(output as SEPL) and stress ratio N (output as SRAT) are computed. The stress ratio is given as
(4–25)
where σe is evaluated using the trial stress . N is therefore greater than or equal to one when yielding is occurring and less than one when the stress state is elastic. The equivalent plastic strain increment is given as:
(4–26)
The equivalent plastic strain and equivalent stress parameters are developed for each option in the next sections.
Note that the Euler backward integration scheme in step 4 is the radial return algorithm (Krieg([46])) for the von Mises yield criterion.
The tangent or elastoplastic stress-strain matrix is derived from the local Newton-Raphson iteration scheme used in step 4 above (Simo and Taylor([155])). It is therefore the consistent (or algorithmic) tangent. If the flow rule is nonassociative (F ≠ Q), then the tangent is unsymmetric. To preserve the symmetry of the matrix, for analyses with a nonassociative flow rule (Drucker-Prager only), the matrix is evaluated using F only and again with Q only and the two matrices averaged.
These options use the von Mises yield criterion with the associated flow rule and isotropic (work) hardening (accessed via TB,BISO).
The equivalent stress Equation 4–4 is:
(4–27) |
where {s} is the deviatoric stress Equation 4–37. When σe is equal to the current yield stress σk the material is assumed to yield. The yield criterion is:
(4–28) |
For work hardening, σk is a function of the
amount of plastic work done. For the case of isotropic plasticity
assumed here, σk can be determined
directly from the equivalent plastic strain of Equation 4–43 (output as
EPEQ) and the uniaxial stress-strain curve as depicted in Figure 4.4: Uniaxial Behavior. σk is
output as the equivalent stress parameter (output as SEPL).
Both the Voce([254]) hardening law, and the nonlinear power hardening law can be used to model nonlinear isotropic hardening. The Voce hardening law for nonlinear isotropic hardening behavior (accessed with TB,NLISO,,,,VOCE) is specified by the following equation:
(4–29) |
where:
| k = elastic limit |
| Ro, |
|
|
The constitutive equations are based on linear isotropic elasticity, the von Mises yield function and the associated flow rule. The yield function is:
(4–30) |
The plastic strain increment is:
(4–31) |
where:
| λ = plastic multiplier |
The equivalent plastic strain increment is then:
(4–32) |
The accumulated equivalent plastic strain is:
(4–33) |
The power hardening law for nonlinear isotropic hardening behavior (accessed with TB,NLISO,,,,POWER) which is used primarily for ductile plasticity and damage is developed in the Gurson's Model:
(4–34) |
where:
| σY = current yield strength |
| σ0 = initial yield strength |
| G = shear modulus |
is the microscopic equivalent plastic strain and
is defined by:
(4–35) |
where:
| εp = macroscopic plastic strain tensor |
|
|
| σ = Cauchy stress tensor |
| : = inner product operator of two second order tensors |
| f = porosity |
This option uses the von Mises yield criterion with the associated flow rule and kinematic hardening (accessed with TB,BKIN).
The equivalent stress Equation 4–4 is therefore
(4–36) |
| where: {s} = deviatoric stress vector |
(4–37) |
where:
|
|
| {α} = yield surface translation vector Equation 4–9 |
Note that since Equation 4–36 is dependent on the deviatoric stress, yielding is independent of the hydrostatic stress state. When σe is equal to the uniaxial yield stress, σy, the material is assumed to yield. The yield criterion Equation 4–7 is therefore,
(4–38) |
The associated flow rule yields
(4–39) |
so that the increment in plastic strain is normal to the yield surface. The associated flow rule with the von Mises yield criterion is known as the Prandtl-Reuss flow equation.
The yield surface translation is defined as:
(4–40) |
where:
| G = shear modulus = E/(2 (1+ν)) |
| E = Young's modulus (input as EX on MP command) |
| ν = Poisson's ratio (input as PRXY or NUXY on MP command) |
The shift strain is computed analogously to Equation 4–24:
(4–41) |
where:
|
|
(4–42) |
where:
| E = Young's modulus (input as EX on MP command) |
| ET = tangent modulus from the bilinear uniaxial stress-strain curve |
The yield surface translation {εsh} is initially zero and changes with subsequent plastic straining.
The equivalent plastic strain is dependent on the loading history and is defined to be:
(4–43) |
where:
|
|
|
|
The equivalent stress parameter is defined to be:
(4–44) |
where:
|
|
Note that if there is no plastic straining ( = 0), then
is equal to the yield stress.
only has meaning during the initial, monotonically
increasing portion of the load history. If the load were to be
reversed after plastic loading, the stresses and therefore
σe would fall below yield but
would register above yield (since
is nonzero).
This option (accessed via TB,PLAS,,,,KINH) uses the Besseling(53) model also called the sublayer or overlay model (Zienkiewicz(54)) to characterize the material behavior. The material behavior is assumed to be composed of various portions (or subvolumes), all subjected to the same total strain, but each subvolume having a different yield strength. (For a plane stress analysis, the material can be thought to be made up of a number of different layers, each with a different thickness and yield stress.) Each subvolume has a simple stress-strain response but when combined the model can represent complex behavior. This allows a multilinear stress-strain curve that exhibits the Bauschinger (kinematic hardening) effect (Figure 4.1: Stress-Strain Behavior of Each of the Plasticity Options (b)).
The following steps are performed in the plasticity calculations:
The portion of total volume for each subvolume and its corresponding yield strength are determined.
The increment in plastic strain is determined for each subvolume assuming each subvolume is subjected to the same total strain.
The individual increments in plastic strain are summed using the weighting factors determined in step 1 to compute the overall or apparent increment in plastic strain.
The plastic strain is updated and the elastic strain is calculated.
The portion of total volume (the weighting factor) and yield stress for each subvolume is determined by matching the material response to the uniaxial stress-strain curve. A perfectly plastic von Mises material is assumed and this yields for the weighting factor for subvolume k
(4–45) |
where:
| wk = weighting factor (portion of total volume) for subvolume k and is evaluated sequentially from 1 to the number of subvolumes |
| ETk = slope of the kth segment of the stress-strain curve (see Figure 4.5: Uniaxial Behavior for Multilinear Kinematic Hardening) |
| Σwi = sum of the weighting factors for the previously evaluated subvolumes |
The yield stress for each subvolume is given by
(4–46) |
where (εk, σk) is the breakpoint in the stress-strain curve. The number of subvolumes corresponds to the number of breakpoints specified.
The increment in plastic strain for each subvolume is computed using a von Mises
yield criterion with the associated flow rule. The section on
specialization for bilinear kinematic hardening is followed but
since each subvolume is elastic-perfectly plastic, C and therefore
{α} is
zero.
The plastic strain increment for the entire volume is the sum of the subvolume increments:
(4–47) |
where:
| Nsv = number of subvolumes |
The current plastic strain and elastic strain can then be calculated for the entire volume via Equation 4–20 and Equation 4–21.
The equivalent plastic strain (output as EPEQ) is defined by Equation 4–43 and equivalent stress
parameter
(output as SEPL) is computed by evaluating the
input stress-strain curve at
(after adjusting the curve for the elastic strain
component). The stress ratio N (output as SRAT, Equation 4–25) is defined using the
σe and
σy values of the first
subvolume.
The material model considered is a rate-independent version of the nonlinear kinematic hardening model proposed by Chaboche([245], [246]) (accessed with TB,CHAB). The constitutive equations are based on linear isotropic elasticity, a von Mises yield function and the associated flow rule. Like the bilinear hardening option, the model can be used to simulate the monotonic hardening and the Bauschinger effect. The model is also applicable to simulate the ratcheting effect of materials. In addition, the model allows the superposition of several kinematic models as well as isotropic hardening models. It is thus able to model the complicated cyclic plastic behavior of materials, such as cyclic hardening or softening and ratcheting or shakedown.
The model uses the von Mises yield criterion with the associated flow rule, the yield function is:
(4–48) |
where:
| R = isotropic hardening variable |
According to the normality rule, the flow rule is written:
(4–49) |
where:
| λ = plastic multiplier |
The back stress {α} is superposition of several kinematic models as:
(4–50) |
where:
| n = number of kinematic models to be superposed. |
The evolution of the back stress (kinematic hardening rule) for each component is defined as:
(4–51) |
where:
| Ci, γi, i = 1, 2, ... n = material constants for kinematic hardening |
The associated flow rule yields:
(4–52) |
The plastic strain increment, Equation 4–49 is rewritten as:
(4–53) |
The equivalent plastic strain increment is then:
(4–54) |
The accumulated equivalent plastic strain is:
(4–55) |
The isotropic hardening variable, R, can be defined by:
(4–56) |
where:
| k = elastic limit |
| Ro, |
The material hardening behavior, R, in Equation 4–48 can also be defined via bilinear or multilinear isotropic hardening options, discussed earlier in Specialization for Bilinear Isotropic Hardening.
The return mapping approach with consistent elastoplastic tangent moduli that was proposed by Simo and Hughes([253]) is used for numerical integration of the constitutive equation described above.
The anisotropic Hill potential theory (accessed by TB,HILL) uses Hill's([50]) criterion (an extension to the von Mises yield criterion) to account for the anisotropic yield of the material. When this criterion is used with the isotropic hardening option, the yield function is given by:
(4–57) |
where:
| σ0 = reference yield stress |
|
|
and when it is used with the kinematic hardening option, the yield function takes the form:
(4–58) |
The material is assumed to have three orthogonal planes of symmetry. Assuming the material coordinate system is perpendicular to these planes of symmetry, the plastic compliance matrix [M] can be written as:
(4–59) |
F, G, H, L, M and N are material constants that can be determined experimentally. They are defined as:
(4–60) |
(4–61) |
(4–62) |
(4–63) |
(4–64) |
(4–65) |
The yield stress ratios Rxx, Ryy, Rzz, Rxy, Ryz and Rxz are specified by the user and can be calculated as:
(4–66) |
(4–67) |
(4–68) |
(4–69) |
(4–70) |
(4–71) |
where:
|
|
Two notes:
The inelastic compliance matrix should be positive definite in order for the yield function to exist.
The plastic slope (see also Equation 4–42) is calculated as:
(4–72) |
where:
| Ex = elastic modulus in x-direction |
| Et = tangent modulus defined by the hardening input |
The following topics concerning Drucker-Prager are available:
This option uses the Drucker-Prager yield criterion with either an associated or nonassociated flow rule (accessed with TB,DP). The yield surface does not change with progressive yielding, hence there is no hardening rule and the material is elastic- perfectly plastic (Figure 4.1: Stress-Strain Behavior of Each of the Plasticity Options (f) Drucker-Prager). The equivalent stress for Drucker-Prager is
(4–73) |
where:
|
|
| {s} = deviatoric stress Equation 4–37 |
| β = material constant |
| [M] = as defined with Equation 4–36 |
This is a modification of the von Mises yield criterion (Equation 4–36 with {α} = {0}) that accounts for the influence of the hydrostatic stress component: the higher the hydrostatic stress (confinement pressure) the higher the yield strength. β is a material constant which is given as
(4–74) |
where:
| φ = input angle of internal friction |
The material yield parameter is defined as
(4–75) |
where:
| c = input cohesion value |
The yield criterion Equation 4–7 is then
(4–76) |
This yield surface is a circular cone (Figure 4.2: Various Yield Surfaces-c) with the material parameters Equation 4–74 and Equation 4–75 chosen such that it corresponds to the outer aspices of the hexagonal Mohr-Coulomb yield surface, Figure 4.6: Drucker-Prager and Mohr-Coulomb Yield Surfaces.
is readily computed as
(4–77) |
is similar, however β is evaluated
using φf (the input
“dilatancy” constant). When
φf = φ, the flow
rule is associated and plastic straining occurs normal to
the yield surface and there will be a volumetric expansion
of the material with plastic strains. If
φf is less than φ
there will be less volumetric expansion and if
φf is zero, there will
be no volumetric expansion.
The equivalent plastic strain (output as EPEQ) is defined by Equation 4–43 and the equivalent
stress parameter
(output as SEPL) is defined as
(4–78) |
The equivalent stress parameter is interpreted as the von
Mises equivalent stress at yield at the current hydrostatic
stress level. Therefore, for any integration point
undergoing yielding (stress ratio (output as SRAT) >1),
should be close to the actual von Mises
equivalent stress (output as SIGE) at the converged
solution.
This option is an extension of the linear Drucker-Prager yield
criterion (input with TB,EDP). Both yield
surface and the flow potential, (input with
TBOPT on
TB,EDP command) can be taken as
linear, hyperbolic and power law independently, and thus
results in either an associated or nonassociated flow rule.
The yield surface can be changed with progressive yielding
of the isotropic hardening plasticity material options, see
hardening rule Figure 4.1: Stress-Strain Behavior of Each of the Plasticity
Options (c) Bilinear
Isotropic and (d) Multilinear Isotropic.
The yield function with linear form (input with
TBOPT = LYFUN) is:
(4–79) |
where:
| α = material parameter referred to pressure sensitive parameter (input as C1 on TBDATA command using TB,EDP) |
|
|
|
|
The yield function with hyperbolic form (input with
TBOPT = HYFUN) is:
(4–80) |
where:
| a = material parameter characterizing the shape of yield surface (input as C2 on TBDATA command using TB,EDP) |
The yield function with power law form (input with
TBOPT = PYFUN) is:
(4–81) |
where:
| b = material parameter characterizing the shape of yield surface (input as C2 on TBDATA command using TB,EDP): |
Similarly, the flow potential Q for linear form (input with
TBOPT = LFPOT) is:
(4–82) |
The flow potential Q for hyperbolic form (input with
TBOPT = HFPOT) is:
(4–83) |
The flow potential Q for power law form (input with
TBOPT = PFPOT) is:
(4–84) |
The plastic strain is defined as:
(4–85) |
where:
|
|
When the flow potential is the same as the yield function, the plastic flow rule is associated, which in turn results in a symmetric stiffness matrix. When the flow potential is different from the yield function, the plastic flow rule is nonassociated, and this results in an unsymmetric material stiffness matrix. By default, the unsymmetric stiffness matrix (accessed by NROPT,UNSYM) will be symmetricized.
The cap model focuses on geomaterial plasticity resulting from compaction at low mean stresses followed by significant dilation before shear failure ([387]). A three-invariant cap plasticity model with three smooth yielding surfaces including a compaction cap, an expansion cap, and a shear envelope proposed by Pelessone ([388]) is described here.
Geomaterials typically have much higher triaxial strength in compression than in tension. The cap model accounts for this by incorporating the third-invariant of stress tensor (J3) into the yielding functions.
Introduced first are functions to be used in the cap model, including shear failure envelope function, compaction cap function, expansion cap function, the Lode angle function, and hardening functions. Then, a unified yielding function for the cap model that is able to describe all the behaviors of shear, compaction, and expansion yielding surfaces is derived using the shear failure envelope and cap functions.
The following topics are covered:
A typical geomaterial shear envelope function is based on the exponential format given below:
(4–86) |
where:
| I1 = first invariant of Cauchy stress tensor |
| subscript "s" = shear envelope function |
| superscript "y" = yielding related material constants |
σ0 = current
cohesion-related material constant (input using
TB,EDP with
TBOPT = CYFUN) |
A, βy,
α
y = material constants
(input using TB,EDP with
TBOPT = CYFUN) |
Equation 4–86 reduces to the Drucker-Prager
yielding function if parameter "A" is set to
zero. It should be noted that all material constants in
Equation 4–86 are defined based on
I1 and
J2 , which are different from
those in the previous sections. The effect of hydrostatic
pressure on material yielding may be exaggerated at high
pressure range by only using the linear term
(Drucker-Prager) in Equation 4–86. Such an
exaggeration is reduced by using both the exponential term
and linear term in the shear function. Figure 4.7: Shear Failure Envelope Functions shows the configuration of
the shear function. In Figure 4.7: Shear Failure Envelope Functions the
dots are the testing data points, the finer dashed line is
the fitting curve based on the Drucker-Prager linear
yielding function, the solid curved line is the fitting
curve based on Equation 4–86, and the
coarser dashed line is the limited state of Equation 4–86 at very high pressures. In
the figure is the current modified cohesion obtained
by setting I1 in Equation 4–86 to zero.
The compaction cap function is formulated using the shear envelope function defined in Equation 4–86.
(4–87) |
where:
| H = Heaviside (or unit step) function |
| subscript "c" = compaction cap-related function or constant |
| R = ratio of elliptical x-axis to y-axis (I1 to J2) |
| K0 = key flag indicating the current transition point at which the compaction cap surface and shear portion intersect. |
In Equation 4–87, Yc is an elliptical function combined with the Heaviside function. Yc is plotted in Figure 4.8: Compaction Cap Function.
This function implies:
When I1, the first invariant of stress, is greater than K0, the compaction cap takes no effect on yielding. The yielding may happen in either shear or expansion cap portion.
When I1 is less than K0, the yielding may only happen in the compaction cap portion, which is shaped by both the shear function and the elliptical function.
Similarly, Yt is an elliptical function combined with the Heaviside function designed for the expansion cap. Yt is shown in Figure 4.9: Expansion Cap Function.
(4–88) |
where:
| subscript "t" = expansion cap-related function or constant |
This function implies that:
When I1 is negative, the yielding may happen in either shear or compaction cap portion, while the tension cap has no effect on yielding.
When I1 is positive, the yielding may only happen in the tension cap portion. The tension cap is shaped by both the shear function and by another elliptical function.
Equation 4–88 assumes that Yt is only a function of σ0 and not a function of K0 as I1 is set to zero in function Ys.
Unlike metals, the yielding and failure behaviors of geomaterials are affected by their relatively weak (compared to compression) tensile strength. The ability of a geomaterial to resist yielding is lessened by nonuniform stress states in the principal directions. The effect of reduced yielding capacity for such geomaterials is described by the Lode angle β and the ratio ψ of triaxial extension strength to compression strength. The Lode angle β can be written in a function of stress invariants J2 and J3:
(4–89) |
where:
| J2 and J3 = second and third invariants of the deviatoric tensor of the Cauchy stress tensor. |
The Lode angle function Γ is defined by:
(4–90) |
where:
| ψ = ratio of triaxial extension strength to compression strength |
The three-invariant plasticity model is formulated by multiplying J2 in the yielding function by the Lode angle function described by Equation 4–90. The profile of the yielding surface in a three-invariant plasticity model is presented in Figure 4.10: Yielding Surface in π-Plane.
The cap hardening law is defined by describing the evolution
of the parameter X0, the intersection
point of the compaction cap and the
I1axis. The evolution of
X0 is related only to the
plastic volume strain . A typical cap hardening law has the
exponential form proposed in Fossum and Fredrich([92]):
(4–91) |
where:
| Xi = initial value of X0 at which the cap takes effect in the plasticity model. |
|
|
Parameters and
have units of 1 / (Force / Length) and 1 /
(Force / Length)2, respectively.
All constants in Equation 4–91 are
non-negative.
Besides cap hardening, another hardening law defined for the
evolution of the cohesion parameter used in the shear
portion described in Equation 4–86 is
considered. The evolution of the modified cohesion
is assumed to be purely shear-related and
is the function of the effective deviatoric plastic strain
γp:
(4–92) |
The effective deviatoric plastic strain γp is defined by its rate change as follows:
(4–93) |
where:
| εp = plastic strain tensor |
|
"
|
| I = second order identity tensor |
The unified and compacted yielding function for the cap model with three smooth surfaces is formulated using above functions as follows:
(4–94) |
where:
| K0 = function of both X0 and σ0 |
Again, the parameter X0 is the intersection point of the compaction cap and the I1 axis. The parameter K0 is the state variable and can be implicitly described using X0 and σ0 given below:
(4–95) |
The yielding model described in Equation 4–94 is used and is drawn in the J2 and I1 plane in Figure 4.11: Cap Model.
The cap model also allows non-associated models for all compaction cap, shear envelope, and expansion cap portions. The nonassociated models are defined through using the yielding functions in Equation 4–94 as its flow potential functions, while providing different values for some material constants. It is written below:
(4–96) |
where:
(4–97) |
where:
| superscript "f" = flow-related material constant |
This document refers to the work of Schwer ([389]) and Foster ([390]) for the numerical formulations used in the Pelessone ([388]) smooth cap plasticity model. ANSYS, Inc. developed a new material integrator that is able to achieve a faster convergence rate for the transition zone between the cap and shear portions.
The flow functions in Equation 4–96 and Equation 4–97 are obtained by replacing
βy, α
y, , and
in Equation 4–94 and Equation 4–95 with
βf, α
f,
, and
. The nonassociated cap model is input by
using TB,EDP with
TBOPT = CFPOT.
Shear hardening can be taken into account on by providing
(via TB,BISO,
TB,NLISO, or
TB,PLAS). The initial value of
must be consistent to
σi - A. This input
regulates the relationship between the modified cohesion and
the effective deviatoric plastic strain.
As the smooth models have more numerical advantages, it is often necessary to transfer nonsmooth caps such as the Sandler model ([387]) to a smooth model. To facilitate the model transformation from the nonsmooth cap model to the Pelessone smooth cap model ([388]), two simple and robust methods are used ([391]); rather than solving a group of nonlinear equations, the ANSYS, Inc. implementation solves only one scalar nonlinear equation.
Calibrating CAP Constants
Calibrating the CAP constants σi,
βY, A, α
Y,
βY, α
F and the hardening input for
differs significantly from the other EDP
options. The CAP parameters are all defined in relation to
I1 and
I2, while the other EDP
coefficients are defined according to p and q.
The Gurson model is used to represent plasticity and damage in ductile porous metals. The model theory is based on Gurson([367]) and Tvergaard and Needleman([368]). When plasticity and damage occur, ductile metal goes through a process of void growth, nucleation, and coalescence. Gurson’s method models the process by incorporating these microscopic material behaviors into macroscopic plasticity behaviors based on changes in the void volume fraction (porosity) and pressure. A porosity index increase corresponds to an increase in material damage, which implies a diminished material load-carrying capacity.
The microscopic porous metal representation in Figure 4.12: Growth, Nucleation, and Coalescence of Voids in Microscopic Scale(a), shows how the existing voids dilate (a phenomenon, called void growth) when the solid matrix is in a hydrostatic-tension state. The solid matrix portion is assumed to be incompressible when it yields, therefore any material volume growth (solid matrix plus voids) is due solely to the void volume expansion.
The second phenomenon is void nucleation which means that new voids are created during plastic deformation. Figure 4.12: Growth, Nucleation, and Coalescence of Voids in Microscopic Scale(b), shows the nucleation of voids resulting from the debonding of the inclusion-matrix or particle-matrix interface, or from the fracture of the inclusions or particles themselves.
The third phenomenon is the coalescence of existing voids. In this process, shown in Figure 4.12: Growth, Nucleation, and Coalescence of Voids in Microscopic Scale(c), the isolated voids establish connections. Although coalescence may not discernibly affect the void volume, the load carrying capacity of this material begins to decay more rapidly at this stage.
The evolution equation of porosity is given by
(4–98) |
where:
| f = porosity |
|
|
The evolution of the microscopic equivalent plastic work is:
(4–99) |
where:
|
|
| σ = Cauchy stress |
| : = inner product operator of two second order tensors |
| εp = macroscopic plastic strain |
| σY = current yielding strength |
The evolution of porosity related to void growth and nucleation can be stated in terms of the microscopic equivalent plastic strain, as follows:
(4–100) |
where:
| I = second order identity tensor |
The void nucleation is controlled by either the plastic strain or stress, and is assumed to follow a normal distribution of statistics. In the case of strain-controlled nucleation, the distribution is described in terms of the mean strain and its corresponding deviation. In the case of stress-controlled nucleation, the distribution is described in terms of the mean stress and its corresponding deviation. The porosity rate change due to nucleation is then given as follows:
(4–101) |
where:
| fN = volume fraction of the segregated inclusions or particles |
| εN = mean strain |
| SN = strain deviation |
| σN = mean stress |
|
|
|
|
It should be noted that "stress controlled nucleation" means that the void nucleation is determined by the maximum normal stress on the interfaces between inclusions and the matrix. This maximum normal stress is measured by σY + p. Thus, more precisely, the "stress" in the mean stress σN refers to σY + p. This relationship better accounts for the effect of triaxial loading conditions on nucleation.
Given Equation 4–98 through Equation 4–101, the material yielding rule of the Gurson model is defined as follows:
(4–102) |
where:
| q1, q2, and q3 = Tvergaard-Needleman constants |
| σY = yield strength of material |
|
|
f*, the Tvergaard-Needleman function is:
(4–103) |
where:
| fc = critical porosity |
| fF = failure porosity |
The Tvergaard-Needleman function is used to model the loss of material load carrying capacity, which is associated with void coalescence. When the current porosity f reaches a critical value fc, the material load carrying capacity decreases more rapidly due to the coalescence. When the porosity f reaches a higher value fF, the material load carrying capacity is lost completely. The associative plasticity model for the Gurson model has been implemented.
Gurson's model accounts for hydrostatic pressure and material isotropic hardening effects on porous metals. The Chaboche model is essentially the von Mises plasticity model incorporating Chaboche-type kinematic hardening.
The Gurson-Chaboche model, also used for modeling porous metals, is an extension of the Gurson model, combining both material isotropic and kinematic hardening. The model is based on the work of Mϋhlich and Brocks ([432]).
The yielding function of the Gurson-Tvergaard and Needleman model is modified as follows:
(4–104) |
where:
Xeff is the total effective back stress, and the total back stress X is the summation of several sub-back stresses:
where the evolution of each sub-back stress is defined by the Chaboche kinematical law:
(4–105) |
The evolution of the equivalent plastic strain is defined through:
This model first requires the input parameters for Gurson plasticity with isotropic hardening, and then additional input parameters for Chaboche kinematic hardening. For more information, see Hardening in the Material Reference.
The cast iron plasticity model is designed to model gray cast iron. The microstructure of gray cast iron can be looked at as a two-phase material, graphite flakes inserted into a steel matrix (Hjelm([335])). This microstructure leads to a substantial difference in behavior in tension and compression. In tension, the material is more brittle with low strength and cracks form due to the graphite flakes. In compression, no cracks form, the graphite flakes behave as incompressible media that transmit stress and the steel matrix only governs the overall behavior.
The model assumes isotropic elastic behavior, and the elastic behavior is assumed to be the same in tension and compression. The plastic yielding and hardening in tension may be different from that in compression (see Figure 4.13: Idealized Response of Gray Cast Iron in Tension and Compression). The plastic behavior is assumed to harden isotropically and that restricts the model to monotonic loading only.
Yield Criteria
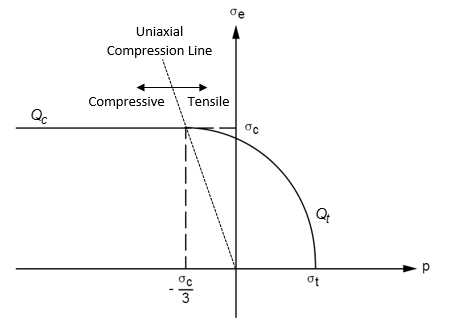
A composite yield surface is used to describe the different behavior in tension and compression. The tension behavior is pressure-dependent and the Rankine maximum stress criterion is used. The compression behavior is pressure-independent and the von Mises yield criterion is used. In principal stress space, the yield surface is a cylinder with a tension cutoff (cap). Figure 4.14: Cross-Section of Yield Surface shows a cross section of the yield surface on principal deviatoric-stress space and Figure 4.15: Yield Surface in the Meridional Plane shows the composite yield surface in the meridional plane.
The yield surface for tension and compression "regimes" are described by Equation 4–106 and Equation 4–107 (Chen and Han([333])).
The yield function for the tension cap is:
(4–106) |
and the yield function for the compression regime is:
(4–107) |
where:
| p = I1 / 3 = tr(σ) / 3 = hydrostatic pressure |
|
|
| S = deviatoric stress tensor |
|
|
|
|
|
|
| σt = tension yield stress |
| σc = compression yield stress |
Flow Rule
The plastic strain increments are defined as:
(4–108) |
where Q is the so-called plastic flow potential, which consists of the von Mises cylinder in compression and modified to account for the plastic Poisson's ratio in tension, and takes the form:
(4–109) |
(4–110) |
where:
|
|
|
|
|
|
|
|
Experimental evidence suggests that is always < 0.5. For
= 0.5, Equation 4–110 reduces to
the von Mises cylinder. The flow potentials in the meridional plane
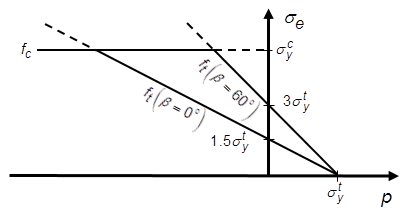
are shown in this figure:
The region to the left of the uniaxial compression line is the compressive flow potential, while the region to the right is the tensile flow potential. As the flow potential is different from the yield function (nonassociated flow rule), the resulting material Jacobian is unsymmetric.
Hardening
The yield stress in uniaxial tension, σt,
depends on the equivalent uniaxial plastic strain in tension,
, and the temperature T. Also the yield stress in
uniaxial compression, σc, depends on the
equivalent uniaxial plastic strain in compression,
, and the temperature T.
To calculate the change in the equivalent plastic strain in tension, the plastic work expression in the uniaxial tension case is equated to general plastic work expression as:
(4–111) |
where:
|
|
The change in the equivalent plastic strain in compression is defined as:
(4–112) |
where:
|
|
The yield and hardening in tension and compression are provided using the TB,UNIAXIAL command which has two options, tension and compression.