Stress analysis on rolling bodies is common in many practical fields. A few examples include vehicle wheels, ball bearings, and rollers in printers. A stress analysis using transient analysis is typically time-consuming. It can be inefficient when fine meshes are necessary for contact analysis. In certain applications where the detailed transient dynamic behavior is not the primary concern, one can significantly simplify the stress analysis with the arbitrary Lagrangian Eulerian (ALE) formulation.
For a rolling body, the mesh for ALE analysis deforms but does not rotate in space; rather, the material flows through the mesh, where a steady-state solution can be obtained for each deformed mesh. An advantage of the non-rotating mesh is that it allows the mesh in the critical region (contact area) to be selectively refined, enhancing simulation efficiency and accuracy.
The following topics related to the ALE formulation and steady state rolling are available:
For further information, including supported element types, see the description of the SSTATE command.
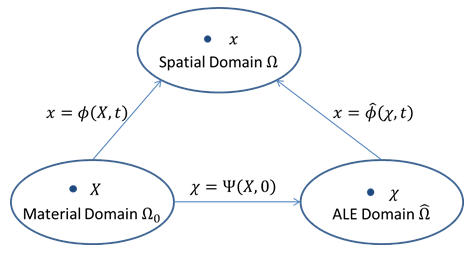
In a finite element analysis based on a Lagrangian mesh, quantities are expressed in both material and spatial domains. Both domains are related via mapping. In the ALE formulation, an additional ALE domain is introduced:
In the ALE formulation, the mesh motion is prescribed or calculated. The inverse map of Ψ is then used to calculate the material motion. The mesh displacement is obtained as:
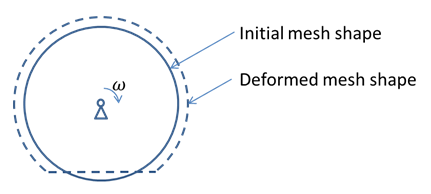
The steady state rolling analysis using ALE formulation is greatly simplified from the general ALE formulation. The following figure shows a body rotating at a constant angular velocity of ω that deforms from the initial shape (solid line) to its steady state deformed shape (dotted line). y
For steady state ALE analysis, all time derivatives vanish in the ALE domain. Specifically, the mesh velocity is shown as:
The material velocity 
is equal to the convective velocity 
, and can
be obtained from the spatial gradient and the referential particle
velocity 
, as shown:
where the referential particle velocity is simply the velocity due to the prescribed material rotation.
Based on the kinematics, the calculation can then be performed in the same way as well established methods for a Lagrangian mesh.
The balance of mass, expressed within the ALE domain, is given by:
where:
 = referential
mass density |
Under steady state, the relative velocity as well as the time derivative vanish. Therefore:
Of special significance is the second
term, where 
. The conclusion therefore is that steady
state rolling, within the ALE framework, is possible only if the body
is homogeneous at least with respect to the axis of rotation, so 
holds.
In this case, the balance of mass is reduced to:
From the balance of linear momentum, the first Piola-Kirchoff, 
, is placed in the ALE domain. Assuming that 
represents the vector
field of body forces, then
is integrated over the volume of the body 
and multiplied by the test function 
to
obtain the weak formulation of the balance of momentum.
Considering the Dirichlet and Neumann boundary conditions, the weak formulation of the equation of motion can be expressed as:
The first and the second term of the left side of the equation
describe the virtual work of the inertial forces and the internal
forces, respectively. On the right side, the virtual work of the volume
forces and the traction 
are considered.
Special attention is given to the inertia term, which inserting the time derivative leads to:
To avoid the higher order gradients that may be obtained inserting again the spatial gradient from the material velocity, Nackenhorst [[429]] proposes that this term be expressed as:
The first term of the right side of the equation describes the steady state rolling that, under steady state conditions, is composed only of first order gradients. The second term is related to the weighted impulse flux going with the convective velocity over the boundary as it vanishes at natural boundaries, common in the continuous formulation of rotating bodies.
For the finite element discretization, the weak formulation of the principle of virtual work which includes the inertia effects is expressed as:
where:
 = tangential stiffness
matrix |
 = inertia matrix |
 = external forces |
 = inertial forces |
 = internal forces |