The Bergstrom-Boyce material model (TB,BB) is a phenomenological-based, highly nonlinear material model used to model typical elastomers and biological materials. The model allows for a nonlinear stress-strain relationship, creep, and rate-dependence.
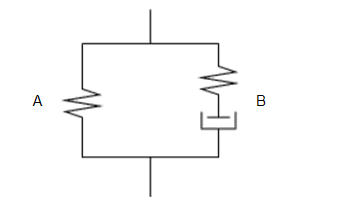
The Bergstrom-Boyce model is based on a spring (A) in parallel with a spring and damper (B) in series, as shown in Figure 4.28: Bergstrom-Boyce Material Model Representation. The material model is associated with time-dependent stress-strain relationships without complete stress relaxation. All components (springs and damper) are highly nonlinear.
The stress state in A can be found in the tensor form of the deformation gradient tensor (F = dxi / dXj) and material parameters, as follows:
 | (4–259) |
where:
 = stress state in A |
 = initial shear modulus of A |
 = limiting chain stretch of A |
 = bulk modulus |
 = det[F] |
 = 
|
 = 
|
 = inverse Langevin function (where the
Langevin function is given by Equation 4–260) |
For numerical efficiency, the Padé ([374]) approximation shown below is used for the inverse Langevin function (). This approximation will differ from the polynomial approximation used for the Arruda-Boyce model.
 | (4–260) |
The stress in the viscoelastic component of the material (B) is a function of the deformation and the rate of deformation. Of the total deformation in B, a portion takes place in the elastic component while the rest of the deformation takes place in the viscous component. Because the stress in the elastic portion is equal to the stress plastic portion, the total stress can be written merely as a function of the elastic deformation, as shown in Equation 4–261:
 | (4–261) |
All variables in this equation are analogous to the variables
in Equation 4–259. The viscous deformation can be
found from the total deformation and the elastic deformation:
Correct solutions for
and
will satisfy:
 | (4–262) |
where:
 = direction of the stress
tensor |
 = effective creep rate |
 = Frobenius norm of the stress
tensor |
 = inelastic network stretch |
 , ε, C, and m = material input
parameters |
As 
is a function of the deformation ( 
), and τ is based on the stress tensor, Equation 4–262 is expanded to:
 | (4–263) |
After Equation 4–263 is satisfied, the corresponding stress tensor from component B is added to the stress tensor from component A to find the total stress, as shown in Equation 4–264:
 | (4–264) |
For more information about the constitutive model, see references [372] and [373]. For more information about the implementation, see reference [374].