*VOPER

*VOPER, ParR, Par1, Oper, Par2, CON1, CON2
Operates on two array parameters.

APDL: Array Parameters

Argument Descriptions

ParR

The name of the resulting array parameter vector. See *SET for name restrictions.

Par1

First array parameter vector in the operation. May also be a scalar parameter or a literal constant.

Oper

Operations:

ADD--: Addition: Par1+Par2.
SUB --: Subtraction: Par1-Par2.
MULT --: Multiplication: Par1*Par2.
DIV --: Division: Par1/Par2 (a divide by zero results in a value of zero).
MIN --: Minimum: minimum of Par1 and Par2.
MAX --: Maximum: maximum of Par1 and Par2.
LT --: Less than comparison: Par1<Par2 gives 1.0 if true, 0.0 if false.
LE --: Less than or equal comparison: Par1 Par2 gives 1.0 if true, 0.0 if false.
EQ --: Equal comparison: Par1 = Par2 gives 1.0 if true, 0.0 if false.
NE --: Not equal comparison: Par1 ≠ Par2 gives 1.0 if true, 0.0 if false.
GE --: Greater than or equal comparison: Par1 Par2 gives 1.0 if true, 0.0 if false.
GT --: Greater than comparison: Par1>Par2 gives 1.0 if true, 0.0 if false.
DER1 --: First derivative: d(Par1)/d(Par2). The derivative at a point is determined over points half way between the previous and next points (by linear interpolation). Par1 must be a function (a unique Par1 value for each Par2 value) and Par2 must be in ascending order.
DER2 --: Second derivative: d²(Par1)/d(Par2)². See also DER1.
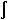
INT1 --: Single integral: Par1 d(Par2), where CON1 is the integration constant. The integral at a point is determined by using the single integration procedure described in the Mechanical APDL Theory Reference.
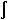
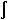
INT2 --: Double integral: Par1 d(Par2), where CON1 is the integration constant of the first integral and CON2 is the integration constant of the second integral. If Par1 contains acceleration data, CON1 is the initial velocity and CON2 is the initial displacement. See also INT1.
DOT --: Dot product: Par1 . Par2. Par1 and Par2 must each have three consecutive columns of data, with the columns containing the i, j, and k vector components, respectively. Only the starting row index and the column index for the i components are specified for Par1 and Par2, such as A(1,1). The j and k components of the vector are assumed to begin in the corresponding next columns, such as A(1,2) and A(1,3).
CROSS --: Cross product: Par1 x Par2. Par1, Par2, and ParR must each have 3 components, respectively. Only the starting row index and the column index for the i components are specified for Par1, Par2, and ParR, such as A(1,1). The j and k components of the vector are assumed to begin in the corresponding next columns, such as A(1,2) and A(1,3).
GATH --: Gather: For a vector of position numbers, Par2, copy the value of Par1 at each position number to ParR. Example: for Par1 = 10,20,30,40 and Par2 = 2,4,1; ParR = 20,40,10.
SCAT --: Scatter: Opposite of GATH operation. For a vector of position numbers, Par2, copy the value of Par1 to that position number in ParR. Example: for Par1 = 10,20,30,40,50 and Par2 = 2,1,0,5,3; ParR = 20,10,50,0,40.
ATN2 --: Arctangent: arctangent of Par1/Par2 with the sign of each component considered.
LOCAL --: Transform the data in Par1 from the global Cartesian coordinate system to the local coordinate system given in CON1. Par1 must be an N x 3 (i.e., vector) or an N x 6 (i.e., stress or strain tensor) array. If the local coordinate system is a cylindrical, spherical, or toroidal system, then you must provide the global Cartesian coordinates in Par2 as an N x 3 array. Set CON2 = 1 if the data is strain data.
GLOBAL --: Transform the data in Par1 from the local coordinate system given in CON1 to the global Cartesian coordinate system. Par1 must be an N x 3 (i.e., vector) or an N x 6 (i.e., stress or strain tensor) array. If the local coordinate system is a cylindrical, spherical, or toroidal system, then you must provide the global Cartesian coordinates in Par2 as an N x 3 array. Set CON2 = 1 if the data is strain data.

Par2

Second array parameter vector in the operation. May also be a scalar parameter or a literal constant.

CON1

First constant (used only with the INT1 and INT2 operations).

CON2

Second constant (used only with the INT2 operation).

Notes

Operates on two input array parameter vectors and produces one output array parameter vector according to:

ParR = Par1 o Par2

where the operations (o) are described below. ParR may be the same as Par1 or Par2. Absolute values and scale factors may be applied to all parameters [*VABS, *VFACT]. Results may be cumulative [*VCUM]. Starting array element numbers must be defined for each array parameter vector if it does not start at the first location, such as *VOPER,A,B(5),ADD,C(3) which adds the third element of C to the fifth element of B and stores the result in the first element of A. Operations continue on successive array elements [*VLEN, *VMASK] with the default being all successive elements. Skipping array elements via *VMASK or *VLEN for the DER_ and INT_ functions skips only the writing of the results (skipped array element data are used in all calculations).

Parameter functions and operations are available to operate on a scalar parameter or a single element of an array parameter, such as SQRT(B) or SQRT(A(4)). See the *SET command for details. Operations on a sequence of array elements can be done by repeating the desired function or operation in a do-loop [*DO]. The vector operations within the ANSYS program (*VXX commands) are internally programmed do-loops that conveniently perform the indicated operation over a sequence of array elements. If the array is multidimensional, only the first subscript is incremented in the do-loop, that is, the operation repeats in column vector fashion "down" the array. For example, for A(1,5), A(2,5), A(3,5), etc. The starting location of the row index must be defined for each parameter read and for the result written.

The default number of loops is from the starting result location to the last result location and can be altered with the *VLEN command. A logical mask vector may be defined to control at which locations the operations are to be skipped [*VMASK]. The default is to skip no locations. Repeat operations automatically terminate at the last array element of the result array column if the number of loops is undefined or if it exceeds the last result array element. Zeroes are used in operations for values read beyond the last array element of an input array column. Existing values in the rows and columns of the results matrix remain unchanged where not changed by the requested operation values. The result array column may be the same as the input array column since results in progress are stored in a temporary array until being moved to the results array at the end of the operation. Results may be overwritten or accumulated with the existing results [*VCUM]. The default is to overwrite results. The absolute value may be used for each parameter read or written [*VABS]. A scale factor (defaulting to 1.0) is also applied to each parameter read and written [*VFACT].

This command is valid in any processor.

Menu Paths

Utility Menu>Parameters>Array Operations>Vector Operations